I never signed up to be a remote learning teacher.
Learning is a social activity and a big part of that is being together to share, discuss, argue, and show our support. It’s difficult to practice social distancing in a school setting. If your picture of a classroom is desks in rows 3 feet apart, with the teacher lecturing and students taking notes and working in quiet isolation, then you need to update your perspective. I’m not saying that isn’t still the case someplace. It’s just not the case for me and many of my colleagues (not just talking about my colleagues at Baxter Academy, either).
This morning, school districts all across Maine have announced that they are closing for the next two weeks, or longer. How do you take an active, noisy, dynamic classroom and transform it into something that can work remotely, with everyone working individually? We’ll muddle through and learn together.
On Friday night I sent this message to my advisory students and their parents:
Hello advisory students (and parents),** This is a long email because I didn’t see you all on Wednesday. Sorry about the length, but I have lots to tell you. Thanks for reading it all the way through. **Well, here we are in uncharted territory. I never signed up to be an online instructor, but that’s what I am now. I promise you that I will try my best to continue to support all of you through this most difficult time.That said, I encourage you to become more engaged with your email. And turn on those Classroom notifications that you’ve turned off. This is the best way to stay informed and stay connected to what’s happening over the next few weeks.I’m not saying that it’s going to be easy. And we have to remember that it’s hard for all of us, teachers and students included. We will all try our best. The thing to remember is that you need to check into Google Classroom to find out what the expectations are for the day, including Flex Friday. As we get better at this new reality, we might be able to post longer term plans for you. In the meantime, understand that we are learning along with you. And be kind. Be kind to each other and be kind to us.Amos’s message implies that all of your classes will be held through Google Meet, a video conferencing app that allows you to log in with everyone else in your class, along with your teacher. I doubt that will happen every day, all day. I suspect that will happen a couple of times during the week, with the other days using Google Classroom posts similar to snow day learning. Your responsibility is really to get your work done. There are “office hours” every afternoon when you can ask your teacher questions – via email or classroom comments or whatever mode your teacher uses. Ms Lucy will be communicating with Mei about the best ways to keep BLC hours, options, and sprint courses going. Take advantage of those opportunities. Do your work. Ask for help. Help others.Several of you are also taking college classes at USM, which will be moving to strictly online following spring break and will stay that way for the rest of their college semester.I’m attaching a graphic that does a good job at explaining online learning etiquette.The good news is that Slate seems to be working, complete with 2nd semester rosters. Give your teachers a chance to upload grades. But at least you will be able to monitor your progress now. Remember, this is about learning. Your teachers will continue to provide you the opportunities to learn – even if it’s in a different mode than what you’re used to or what you prefer. Only you can take advantage of the opportunities we provide. (Speaking for my colleagues, based on conversations from today, we would prefer to be with you live and in person.)I anticipate that you will be asked to give some feedback on the processes that we are testing out and trying to use through this difficult time. Give your feedback and use your voice.The digital learning schedule is also attached. Remember, the main thing is doing the work. It’s nice for you to “show up” if your teacher invites you to a Google Meet session. It makes us feel like you care and value us. But, if that’s not possible for you to do, then be sure to do the work and turn it in on Classroom. That’s going to be our main mode of communication. So show up, check in, and be present.Unless you are feeling sick, nothing about what we’re doing mandates that you stay home while we are learning this way. That said, we are all trying really hard to slow the transmission of this thing, so use your best judgement – stay out of crowded areas, but go outside and soak up some sunshine; practice good hygiene, but don’t shake hands; if you work in retail, wash your hands a lot, seriously.Like I posted on our Advisory classroom, let me know if you have any questions or need my support in any way. This is going to be new for us all and we need to support each other. I am grateful that you are my advisory and I am grateful for your parents’ support.Be well and I hope to see you all soon.


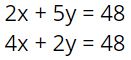
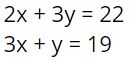
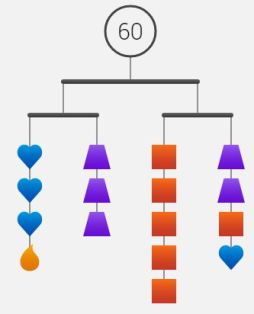




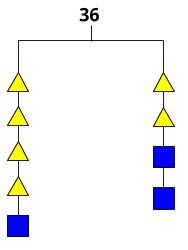
 Looking closer at the center mobile, students used the same “cross out” method to find the relationship that 2 triangles equals 3 squares. If we’d been teaching the substitution method in a more traditional way, kids would have been pushed to figure out how much 1 triangle (or 1 square) was worth before making the substitution step. We knew substitution was happening here, but we didn’t invent this approach so we just followed closely to see where our students took us. Since 2 triangles equals 3 squares, some kids substituted 3 squares for the two triangles on the right branch of the mobile. Others made two substitutions of 6 squares for the 4 triangles on the left branch. Either way the result was a branch of 7 squares that totaled 14. It seemed quite natural to them.
Looking closer at the center mobile, students used the same “cross out” method to find the relationship that 2 triangles equals 3 squares. If we’d been teaching the substitution method in a more traditional way, kids would have been pushed to figure out how much 1 triangle (or 1 square) was worth before making the substitution step. We knew substitution was happening here, but we didn’t invent this approach so we just followed closely to see where our students took us. Since 2 triangles equals 3 squares, some kids substituted 3 squares for the two triangles on the right branch of the mobile. Others made two substitutions of 6 squares for the 4 triangles on the left branch. Either way the result was a branch of 7 squares that totaled 14. It seemed quite natural to them.


